Дисперсията на формула дисперсия, вида на дисперсията, прост дисперсия на претеглената дисперсията

Концепцията на дисперсия

Различията в статистиката е средното квадратично отклонение на отделните характерните стойности в квадрата на средната аритметична. В зависимост от първоначалните данни, се определя от прости формули и претеглените разлики:

1. Обикновено дисперсия (за разгрупирани данни) изчислява по формулата:

2. претеглена дисперсията (за редица вариации):

където п - честотата (повторяемост фактор X)

Пример дисперсия констатация

На тази страница описва стандартната пример за намиране на дисперсията, можете да видите и други задачи на своята констатация

Пример 1. Следващите данни за група от 20 ученици от отдела за кореспонденция. Ние трябва да се изгради редица характерни интервал дистрибуция, изчисляване на средната стойност на знака и разгледа неговата дисперсия

Ние изгради група интервал. Ние дефинираме на завъртане гамата с формула:

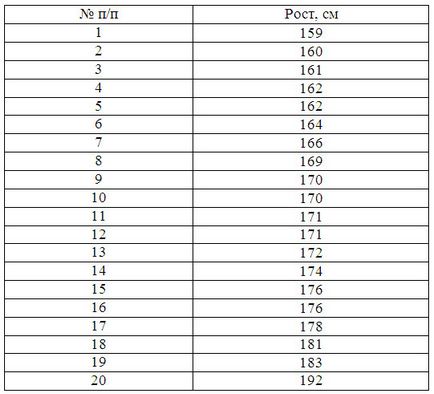
където X Макс максимална функция група;
X мин минимална стойност групиране функция;
п - номер на интервали:

Ние приемаме п = 5. Етап равен на: з = (192-159) / 5 = 6.6

Форма на интервал групата

За допълнителни изчисления се изгради спомагателни таблица:

X'i- средата на интервала. (Например среден клас 159 - 165,6 = 162.3)

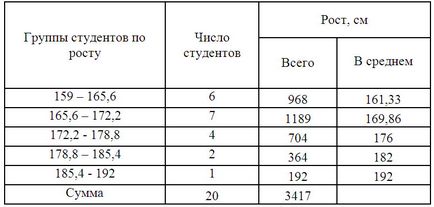
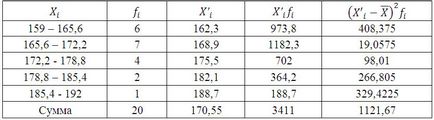
Средната стойност на студенти растеж по формулата претеглена средна аритметична:

Ние дефинираме дисперсията съгласно формулата:

дисперсия формула може да се трансформира, както следва:

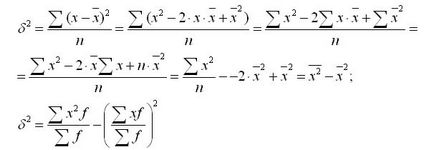
От тази формула следва, че средата за дисперсия е равна на разликата на квадрати и квадратна изпълнение и средното.

Дисперсия в вариационни редове на равни интервали по метода на моменти следните метод може да се изчисли с помощта на втори дисперсионни свойства (разделящи всички варианти на големината на интервала). Определяне на дисперсията. изчислява по метода на моменти, следната формула по-малко трудоемък:

където I - стойността на интервала;
А - номинална нула както е удобно използва средната интервал като най-голяма честота;
m1 - квадратни точки в първата поръчка;
m2 - втори ред момент

Дисперсията на алтернативен знак (ако статистическа знак населението се променя, така че има само две взаимно изключващи изпълнение, такава променливост, наречена алтернатива) може да се изчисли по формулата:

Заместването на тази дисперсия формула р = 1 р, ние получаваме:

видове дисперсия

Общата вариация измерва вариация характеристика на цялото население като цяло под влиянието на всички фактори, отговорни за този вариант. Тя е равна на средното квадратично отклонение на отделните стойности на характеристика х общата средна стойност на х и може да се определи като обикновен дисперсия или претеглена вариацията.

В рамките на група вариацията характеризира произволно отклонение, т.е. на отклонението, което се дължи на влиянието на незаписани фактори и не зависи от характерните фактор, лежащ в основата група. Тази вариация е средната квадратична стойностите на грешките разделят функция в рамките на групата X от средната аритметична стойност на групата, и могат да бъдат изчислени като просто като претеглена вариацията или дисперсия.

Така, в рамките на дисперсия характерни мерки промяната в рамките на групата и е дадено от:

където Xi - средната стойност на група;
Ni - броят на единиците в групата.

Така например, в рамките на група вариация, която трябва да бъде определена в задачата за изучаване на въздействието на уменията на работниците до нивото на производителността на труда в магазин покажи вариации на продукцията във всяка група, причинени от всички възможни фактори на (техническо състояние на оборудването, осигуряване на инструменти и материали, възрастта на работниците, интензивност на труда и т.н. .), с изключение на разликите в квалификациите изхвърлянето (в рамките на групата всички работници имат същите квалификации).

Средно на вътрешно-групови разрез отразява случайни изменения. Т. Е. Ту част на промяната, които се появяват под влиянието на други фактори, с изключение на фактор група. Тя се изчислява, както следва:

Смесената дисперсия характеризира систематично отклонение Получената променлива, която се дължи на влиянието на фактора функция, лежащ в основата група. Тя е равна на средната квадратна отклонение на груповите средни стойности от общата средна стойност. Между група отклонение се изчислява както следва:

Обикновено прибавяне на дисперсия в статистика

Съгласно принципите на добавяне на отклонения общо вариацията е сумата от средната стойност на дисперсията на рамките и между група:

Точката на това правило е, че общата дисперсия, която се среща под влиянието на всички фактори, е сумата от променливите, които се появяват под влиянието на всички други фактори, и дисперсията, която се проявява чрез групиране фактор.

С помощта на формулата дисперсии на допълнение може да се определя от два известни дисперсии трети неизвестен, и съди устойчивостта на удар, функция за групиране.

дисперсионни свойства

1. Ако всички намаляването характерната стойност (увеличение) на същата постоянна стойност, тогава отклонението няма да се промени.
2. Ако всички стойности на намаляване функция (увеличение) на същия брой пъти п, дисперсията съответно ще намалее (увеличение) в п ^ 2 пъти.