Паралелограма - четириъгълник чиито противоположни страни са успоредни.
Теорема (свойства успоредник):
успоредник срещуположните страни са равни и противоположни ъгли са равни: ,,,.
Диагоналите на успоредник разполовявам пресечната точка :.
Ъгли, съседни на всяка страна, в количество равно.
Диагоналите на успоредник я разделят на две равни триъгълници.
Сумата от квадратите на диагоналите на успоредник е равна на сумата от квадратите на страните му :.
Ако противоположните страни на четириъгълник са успоредни, тогава четириъгълник - успоредник.
Ако четириъгълник срещуположните страни са равни, а след това на четириъгълник - успоредник.
Ако четириъгълник двете срещуположни страни са равни и успоредни, а след това на четиристранни - успоредник.
Ако четириъгълник диагонал преминаване, пресечната точка разделя на половина, след това този четириъгълник - успоредник.
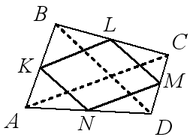
Средите на случаен принцип (включително не-изпъкнала или пространствен) са върховете на четириъгълник успоредник Pierre Varignon.
Страните на успоредника са успоредни на диагоналите на четириъгълника. Пиер Varignon успоредник периметър, равен на сумата от дължините на диагоналите на четириъгълник източник, а площта на успоредника Пиер Varignon равна на половината от площта на оригиналната четириъгълник.