характеристика сила

Силата обикновено зависи от времето, позицията на точка и скоростта:

1. POWER, в зависимост от времето:

От електрическа интензивността на полето в точка електрически заряд действа сила. Ако силата на електричното поле зависи от времето, силата, действаща по обвинение в точка ще зависи от времето:

Чрез сили на този клас, но действа между материалните тела могат да включват, например двигател с възвратно-постъпателно движение на частите действа към основата. В много случаи тези сили имат периодичен характер и, следователно, да се появи тригонометрични функции.

2. POWER, в зависимост само от скоростта на точката:

С тези сили, което най-често се сблъскват, когато се разглежда движението на тялото в една устойчива среда. Силата на съпротива от страна на околната среда се извършва само, когато има движение на тяло спрямо средата. Когато относителната скорост е нула, съпротивителната сила изчезва. Тази сила е насочена противоположно на скоростта на тялото. устойчивост сила зависи от скоростта на тази зависимост в общия случай е сложна. Въпреки това, с бавно движение на относителната устойчивост сила на тялото пропорционално на скоростта:

където # 955; - коефициент на пропорционалност в зависимост от свойствата на средата (в случай на движение на телата # 955; Това зависи от формата и размерите на тялото). При по-високи скорости, тази зависимост е неправилно. В този случай, не е квадратна или хидравличен закон съпротива:

където к - коефициент на пропорционалност зависи от същите фактори като това.

При много високи скорости, този закон е станала по-сложна, но с достатъчна степен на точност може да се приеме, че силата на устойчивост на движение на точка в течност или газ зависи само от скоростта и посоката, противоположна на нея.

СИЛА, в зависимост само от позицията на точката:

От особено значение са два вида правомощия от този клас: еластичната сила и гравитационната сила.

а) еластичната сила

еластичните сили, генерирани по време на деформацията на еластични тела. Пример на еластичната сила може да бъде силата, произтичащи когато пружината е деформиран. Когато пролетта е в свободно състояние - силата е равна на нула. Но ако през пролетта, за да се разтяга или свива, тя се превръща в сила, която се опитва да го върне в първоначалното си състояние.

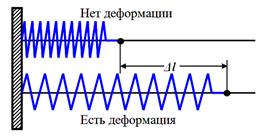
За пружина, при което # 8710; л - удължение, к - коефициент на пропорционалност - пролет коефициент твърдост.

| л | не е задължително функция на еластичната сила (например, конична пружина тази зависимост не е линейна.) Въпреки това, в повечето практически проблеми трябва да се счита еластична сила, пропорционално на деформация.

N закрепваща точка определена относителна XYZ. - радиусът вектор от точка М в отсъствието на деформация на пружината - радиусът вектор от точка М в присъствието на пружина деформация. За еластичната сила:

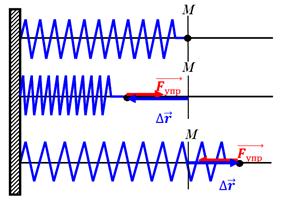
Знакът "-" означава, че силата е насочена срещуположно на вектора.

Един вектор уравнение, изразяващо закона на Хук, което се равнява на три уравнения в прогнозите:

Ако позицията на точка М в отсъствието на деформация съвпада с произхода 0 на координатната система, предишното уравнение може да се запише като:

Ако оста на симетрия на пружината да се комбинират една от осите на декартовата координатна система (например, 0X ос), ние получаваме на едномерен случай на проблема:

б) гравитационната сила

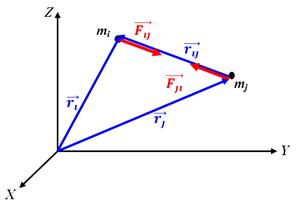
Гравитационната сила - сила, определена от закона за всемирното привличане. отворен I. Нютон (1678): две съществени точки са привлечени един към друг със сила, пропорционална на масата на материал, а и обратно пропорционална на квадрата на разстоянието между тях;

или, където - вектора, изготвен от материал, точка маса МП в точка маса материал мл. - радиус вектор пространство определено от положението на точката, в която материал точка маса ИН. - радиус вектор пространство определено от положението на точката, в която материал точка маса МП. = 6,67. 10 - 11 часа. m2 / кг 2 - тежестта константа (първата е определено в 1798 от Хенри Кавендиш).

Гравитационната сила взаимодействие на двете материални тела се определя от съотношението:

Всички теми на този раздел:

Механика - наука за движение и равновесие на телата.
Под механично движение разбере промяна в позицията на телата в пространството с течение на времето. Знайте tela- на движение

Твърдо тяло - тялото, разстоянието между две точки, които, по време на движение остава непроменено.
Пространството описано Euclidean геометрия. Най-важните свойства на пространството - еднаквост (същите свойства на пространството в нейните различни области);

точка на скоростта и неговото присъствие на различни начини на движение на точката
Важен параметър, който характеризира движението е точката на скоростта на движение. Ние считаме, че движението на точката, тъй като вектор уравнение за определянето на това понятие:

Специфични случаи на точката
Еднакво праволинейно движение равномерно праволинейно движение е математически дефинирани uravneniemNayde

Комплекс за движение на точка
За движение на тялото се съди по движението на всяка точка. По-рано ние счита движението на точка в координатната система, която е условно се приема, фиксиран. Въпреки това, на практика, трябва да се п

Транслационно движение на твърдо тяло
Ние първо да обмислят простите случаи на движение - напред за движение на твърдо тяло и твърда въртене на тялото.

Ротация абсолютно твърдо тяло около на фиксирана ос
Ние се определи две точки ДТО. Помислете колко трудно ще се движат всички точки на тялото и да научат как да се определи скоростта и началото

Въртенето на твърдо тяло с постоянно ъглово ускорение
Нека да видим как това движение ще бъде написана, когато кинематична уравнението на движение на тялото. Първоначално се получи формула, чрез която е възможно да се намери ъгловата скорост на тялото в този случай. 0z изпрати по оста

В общия случай движения на твърдо тяло
Ние показваме, че всяко движение на твърдо тяло може да бъде представена като сумата на двете си движения: транслацията и въртене. Нека тялото се движи по произволен начин. Различаваме

кинетика
В изучаването на кинематиката на движението на телата се разглеждат като се има предвид, и ние не се интересуват от причината за кауза или промяна на движението. Нека сега се обърнем към изучаването на причините, които определят механичните

Материална точка магазини за състоянието на покой или равномерно праволинейно движение, докато, докато някои сила няма да се промени това състояние.
Тази аксиома гласи, че за движението на постоянна величина, и посоката на скоростта не се нуждае от енергия. Този проблем не се ограничава само до правото на инерцията. законът казва за мир или

Механичната принципа на относителността
Уравнението, който изразява основния закон на динамиката ясно показва, че този закон не може да бъде справедливо за всеки,

динамиката на материална
Въз основа на аксиоми на механиката, динамиката се развива главно на разследването на втората аксиома, която поради това се нарича основният закон на динамиката. Основният закон на динамиката е формулиран за един

И законите на опазването
Общи теореми на динамиката на материална точка е логично следствие от основния закон на динамиката на материалните обекти. обикновено

В работната сила. мощност
Да предположим, че една сила действа върху подложка

Теорема на промяна на кинетичната енергия.
Помислете за движение на точка под действието на сила. Динамичният уравнението на движение на частиците може да се запише като:

Закон за запазване на инерцията на системата.
Да разгледаме първата система, състояща се от N масови точки, всяка от които взаимодейства с друг. В допълнение, материалните точки на системата могат да работят материална точка

Теорема на движението на масовия център
центъра на маса или център на инерция на система, състояща се от N масови точки се нарича геометрична точка, положението на които се определя от вектора на радиус

Закон за запазване на момента на импулса на механична система.
Нека първо разгледаме система, състояща се от п материални точки. Нека пишат основния закон на динамиката за всяка точка:

Закон за запазване на общата механична енергия на системата.
Нека пишат основния закон на динамиката за всяка точка. к = 1, 2, 3, ..., п. В скаларен продукт на това уравнение п

ДИНАМИКА абсолютно стабилно.
Произволното твърда движение на тялото може да се опише от две теореми - за промяна на относителната ъглова инерция на центъра на масата и теоремата на центъра на масово движение.

Динамика на постъпателно движение на твърдо тяло.
Когато движението напред на всички точки на твърдото тяло се движат едни и същи, така че знам как точно тя ще се премести

Динамиката на твърдо тяло въртене около фиксирана ос.
Кинетичната енергия на въртящ твърдо тяло Първо, ние откриваме израз за кинетичната енергия на материал точка, въртящи се с ъгловата скорост

Основният уравнение на динамиката на въртеливото движение
Нека твърдо тяло се върти около фиксирана ос съвпада с оста 0z. На тялото на активното сила е