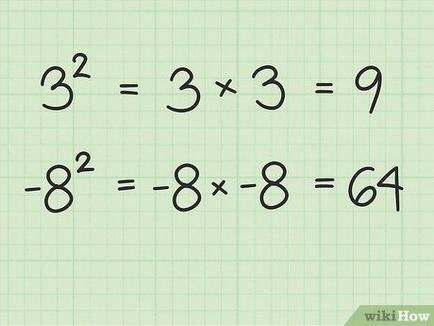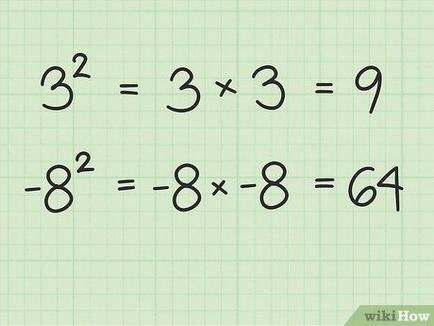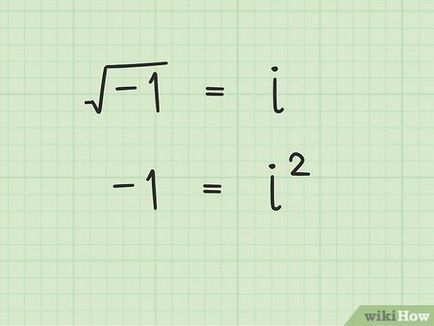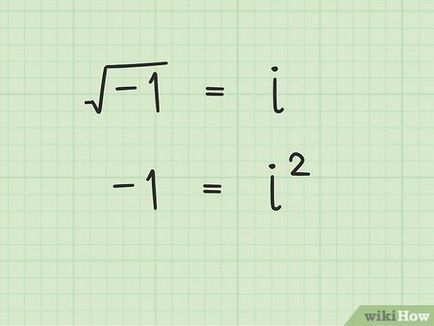Въпреки че страшно оглед на корен квадратен символ, и може да направи човек се свият, а не силни в математиката, квадратен корен на проблема не е толкова трудно, колкото може да изглежда първата. Простите задачи с корен квадратен често могат да бъдат решени толкова лесно, колкото на обикновените задачи с умножение или деление. От друга страна, по-сложните проблеми могат да изискват известни усилия, но с правилният подход, дори и те не ви накара да работи. Започнете да се реши проблема от корен днес, за да научите как това радикално нов математически умения!
стъпки Редактиране
Част 1 от 3: Разбиране на броя на площади и корен квадратен Редактиране
брой повдигане на квадрат, като се умножава по себе си. За да се разбере квадратни корени, по-добре е да се започне с квадратите на номера. Квадрати на числа е съвсем проста: изграждане на площада означава, че той се умножи по себе си. Например, 3 на квадрат е същата като на 3 х 3 = 9, а 9 в кутията е същата като на 9 × 9 = 81 квадратчета с малко писане на цифрата "2" вдясно от издигане на квадратен номер са отбелязани. Пример 3. 2. 9 2. 100 2 и така нататък.
- Опитайте сами да квадрат още няколко числа, за да изпробват на концепцията. Не забравяйте, че изграждането на площада означава, че този брой трябва да бъде умножена по себе си. Това може да стане дори и за отрицателни числа. В този случай, резултатът винаги е положителен. Например: 2 -8 = -8 х -8 = 64.
Когато става въпрос за квадратните корени, има обратен процес на квадратура. корен символ (√, тя се нарича още радикален) по същество означава обратното на характера 2. Когато видите радикала, трябва да се запитате: "Какво брой може да бъде умножена по себе си, за да получите по-долу от корена?". Например, ако видите √ (9), тогава трябва да се намери число, което, когато се изправи, за да се даде номер девет. В нашия случай, този брой е три, тъй като 02 Март = 9.
- Помислете за друг пример и да разберете главната 25 (√ (25)). Това означава, че ние трябва да намерим номер, който ще бъде на площада ни даде 25. От 5 2 = 5 × 5 = 25, можем да кажем, че √ (25) = 5.
- Можете също така да мисля за него като за "отмяна" квадратура. Например, ако ние трябва да намерим √ (64), корен квадратен от 64, нека да мислим за този номер, тъй като 8 2. Като корен символ "Отказ", квадратура, можем да кажем, че √ (64) = √ (8 2) = 8.
Знайте, разликата между идеал и перфектно квадратура. До тогава, отговорът на нашия проблем, като корените са хубави и кръгли числа, но това не винаги е така. Отговорите на корен квадратен от проблеми могат да бъдат много дълги и неудобни с десетична дроб. Брой, в основата на която е числа (с други думи, числата, които не са заснети), наречени добра площади. Всички от горните примери (9, 25 и 64) са перфектни квадрати защото тяхната коренова е цяло число (3,5 и 8).
- От друга страна, броят на които в изграждането на корените не се отказвайте от цяло число, наречено непълни квадрати. Ако сложите един от тези номера в основата, можете да получите номер с десетична дроб. Понякога този номер може да бъде много дълъг. Например, √ (13) = 3,605551275464.
Не забравяйте първо 1-12 от квадрати. Както вероятно вече сте забелязали, за намиране на корен на точен квадрат е доста лесно! Поради факта, че тези проблеми са прости да се помни корените на първата дузина квадрати. Вие не просто излезе с тези номера, така че отделете малко време, за да си спомнят рано и да спести време в бъдеще.
- 01 февруари = 1 × 1 = 1
- 2 2 = 2 х 2 = 4
- 03 Февруари = 3 х 3 = 9
- 4 2 = 4 х 4 = 16
- 5 2 = 5 х 5 = 25
- 6 2 = 6 х 6 = 36
- 07 февруари = 7 × 7 = 49
- 2 авг = 8 х 8 = 64
- 02 сеп = 9 х 9 = 81
- Февруари 10 = 10 × 10 = 100
- 11 февруари = 11 х 11 = 121
- Февруари 12 = 12 х 12 = 144
Използването на имагинерните числа, да открие корена на отрицателно число. Задайте си въпроса, какво число, умножено по себе си дава -16? Това не е 4 или -4, тъй като изграждането на тези номера на площада ще ни даде положително число 16. предал? В действителност, няма начин да се запиша в основата на -16 или друга отрицателна брой обикновени числа. В този случай, ние трябва да се замени с имагинерни числа (обикновено под формата на букви или символи), че те са били на мястото на корен от отрицателно число. Например променливата «I» обикновено се използва за изграждане на корен на -1. Обикновено основата на отрицателно число винаги имагинерно число (или включени в него).
- Имайте предвид, че въпреки че въображаемите номера и не могат да бъдат осигурени от традиционните номера, те все още могат да бъдат третирани като такива. Например, корен квадратен от отрицателно число може да бъде квадрат до получаване на тези отрицателни числа, като всеки друг, квадратен корен. Например, I 2 = -1