координатна линия

Вземете обичайната линия. Ние я наричаме преки х (Фиг.1). Ние избираме този пряк отправна точка О, и стрелката да показва положителна посока на тази права линия (фиг. 2). По този начин, в дясно от точка O ние сме положителни числа, а отляво - отрицателна. Ние избираме мащаба, т.е. размера на прав участък от един. Обърнахме се координира линия (фиг. 3). Всяко число съответства на определена една точка на линията. И този номер се нарича координатите на тази точка. Ето защо, директен и координира обади. Еталон О се нарича произхода.

Например, на фиг. 4, точка Б е на разстояние от 2 до правото на произхода. Точка D се намира на разстояние от 4 до лявата страна на произход. Съответно координатна точка В е 2, и точка D координира -4. Самата точка е О, като отправна точка координира е 0 (нула). Тя обикновено се изписва като: О (0), В (2), D (-4). И постоянно да казва "точка D, за да координира такава" говори лесно "точка 0, точка 2, буква -4". А самата точка а е достатъчно да се определи координата (фиг. 5).

Знаейки, координатите на две точки от оста на координатната, винаги можем да се изчисли разстоянието между тях. Да предположим, че имаме две точки А и Б с координати А и В съответно. Разстоянието между тях е, | а - б. | Запис | а - б | Тя се чете като "моден б минус" или "модул на разликата на числата а и б».

Алгебрично единица х - е неотрицателно цяло число. Наричана | х |. И ако пространството х> 0, тогава | х | = X. Ако х <0, то |x| = -x. Если x = 0, то |x| = 0.

Геометрично модул на х - разстоянието между точката и произхода. И ако има две точки с координати x1 и x2, както | x1 - x2 | - разстоянието между тези точки.

Модулът се нарича още като абсолютна стойност.

Какво друго можем да кажем, когато става въпрос за оста на координатната? Разбира се на числови интервали.

Видове числови интервали.

Открит лъч.
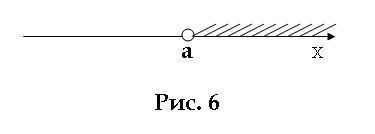
Да кажем, че имаме две числа а и б. Където В> а (б повече от една). На оста на координатната, това означава, че точка Б се в дясно на. Ние замени нашата неравенство б в променливата х. Това означава, че х> а. Тогава х - това е всичко това е повече от броя на. На оста на координатната е съответно всички точка на правото на. Тази част на излюпени линии (фиг. 6). Този набор от точки се нарича отворена лъч. и активен цифров интервал, определен (а + ∞), където знакът + ∞ чете като "положителен безкрайност". Имайте предвид, че самата точка не е включена в даден период и е обозначен с отворени кръгове.

Затворен лъч.
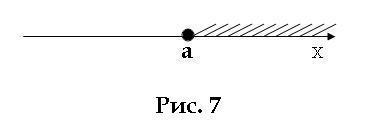
Ние също разгледаме случая, когато х ≥ а. Тогава х - е всички номера, по-голямо или равно на. На координатна линия е всички точки на правото и, както и много точка а (фиг. 7, точка вече посочено от тъмно кръг). Този набор от точки се нарича затворен лъч (или светлина) и числения интервал означен [а; + ∞). Имайте предвид, че ние използваме квадратни скоби, което означава, че принадлежи на определен интервал от време.

Интервал.
Сега вземайте двойна строго неравенство

Интервал.
За леко модифицираме неравенство на ≤ х

Сегмент.
И накрая, ние приемаме двойното неравенство nonstrict а ≤ х ≤ б. Къде х - е всички номера, по-голямо или равно на, и по-малка или равна на б. На координатна линия е всички точки между точките А и В (фиг. 10), както и самите а и б точки. Този набор от точки се нарича сегмент. и активен цифров интервал означен [а; Ь].

Координира ос се нарича ос на координатната. Или просто оста х.