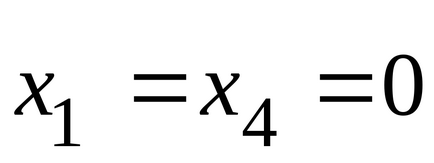Общи правила за съставяне на двойните проблеми

Правило 1: Всички ограничения на първоначалния проблем свободни членове трябва да са от дясната страна, както и членовете с неизвестен - от лявата.

Правило 2. Първоначалният проблем на ограниченията-неравенство трябва да бъдат написани така, че неравенството признаци, че са в една и съща посока.

Правило 3. Ако неравенството знаци ограниченията на първоначалния проблем "

"Целевата функция и ако""Тогава.

Правило 4. Всеки ограничение проблем неизвестен източник съответства на двойната проблема, неизвестен съответното ограничение, неравенството трябва да отговаря на условието за не-негативност и неизвестни съответните ограничения равенство може да бъде или знак.

Правило 5. Целевата функция на двойния проблем има формата

,

където

- свободни термини в ограниченията на първоначалния проблем.

Правило 6. целевата функция

Тя трябва да бъде оптимизиран в сравнение с обратнотоначин.

Правило 7. Всяка neizvestnomuhj, к = 1, 2, ..., п първоначалният проблем съответстваща на границата на два проблема. Наборът от ограничения etihn (заедно с неотрицателност neizvestnyhyi условия. Неравенства-подходящи ограничения на първоначалния проблем) форми на ограничения на системата двоен проблем. Всички ограничения на двоен проблем имат формата на неравенството, свободни членове, които са в страни от дясната, и с членове на neizvestnymiy1, y2. ...,

- в ляво.

Всички неравенство признаци са от вида "

"Ако и""Тогава.

6.2. Едновременно разтвор на първичните и двойни проблеми

Едновременно разтвор на първичните и двойни проблеми се основава на теорията на дуалността. Duality теореми ни позволяват да се установи връзка между оптималното решение на чифт двойни проблеми. Вземането на решение един от чифт двойни проблеми, или можете да намерите оптималното решение на друг проблем, а не да го решите или да зададете негово отсъствие. В следните случаи:

- двата проблема на двойна двойки са оптимални решения;

- един от проблемите не е решение в очите на целевата функция е неограничено, а другият няма решение с оглед на несъвместимост на системата от ограничения.

Теорема 6.2.1 (1-во двойственост теорема). Ако една от целите на двойна двойка взаимно разтворими, на решими и други предмети, в този случай на оптимални стойности на обективни функции са еднакви. Ако целевата функция е една от целите не се ограничава до (най-горе - да се увеличи максимално проблема от дъното - с цел минимизиране на проблема), набор от изпълними планове за други задачи е празен.

Тази теорема предполага следното

Следствие. С цел да се изпълними решения

и





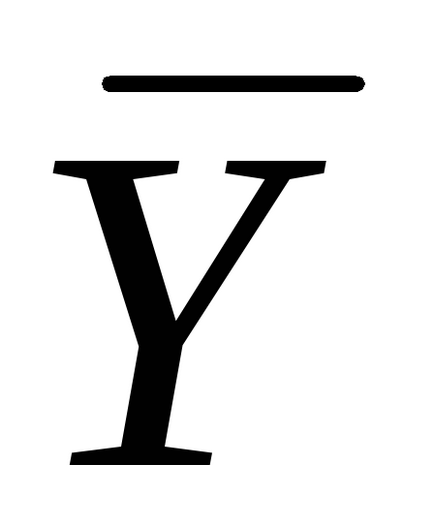
двоен чифт проблеми са оптимално, е необходимо и достатъчно обективната функция на тези равнини съвпадат.

Теорема 6.2.2 (2-ри двойственост теорема). Да бъде симетричен чифт двойни проблеми

, ;,.

За да възможни решения, е оптимално решение двойката двойна проблеми, е необходимо и достатъчно следните уравнения:

В противен случай, ако заместването на оптималното решение в I-ия ограничения ограничават първоначалната задача се изпълнява като строго неравенство, TOI-координата на оптималното решение на двойната проблем е нула, и обратно, eslii координата на оптималното решение на двойната проблем е различно от нула, toi- т.е. ограничаване на първоначалния проблем оптималното решение е изпълнено като равенство.

Пример 6.2. За този проблем да се направи двойна решаване на графичния метод и използване на втори двойственост теорема, за да се намери решение на първоначалния проблем:

, .

Решение. Ние построи двойна проблема

Ние се реши този проблем, като графичен метод. Фиг. 6 показва границите на допустимите решения на проблема, нормалата

ниво линии, линии ниво и оптимално решение.

,

;

, ;

;

.

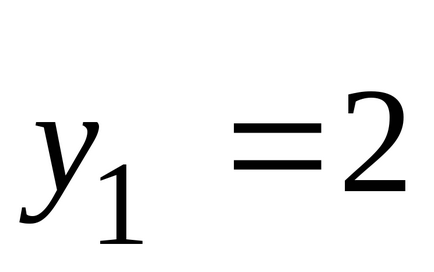
Замести оптималното решение

в ограничения. Ние считаме, че ограниченията (1) и (4) се изпълняват като строго неравенство:

Съгласно втория дуалността теоремата на съответните координати на оптимално двойна разтвор, т.е. първоначалният проблем са равни на нула:

. С оглед на това, първоначалният проблема с ограниченията на системата се

;