Vertex (геометрия)
Vertex на ъгъла - това е точката, Окуда произхождат две греди.
Vertex на ъгъла - това е мястото, където двете греди произход; където двата сегмента се събират; където двете линии се пресичат; където всяка комбинация от греди и прави сегменти, съставляващи двете (прости) "страни", които се събират в една точка [2].
полихедронов полигон
Peak - е крайъгълният точка на полигона или многостен (всякакъв размер), с други думи своите 0 триизмерни лица.
връх на многоъгълник се нарича "изпъкналата", ако ъгълът е по-малко от радиани вътрешната многоъгълни пи (180 ° - две прав ъгъл). В противен случай връх се нарича "вдлъбнат".
По-общо, връх на многостен е изпъкнал Стол ако пресичане с достатъчно малка площ. с връх като център, е изпъкнала форма; друго, връх е вдлъбната.
Върховете на многостен свързани с върховете на графиката. от многостен е графика, чиито върхове съответства на върховете на многостен [3]. и следователно, графиката на многостен може да се счита като едномерен симплициален комплекс. чиито върхове са върховете на графиката. Въпреки това, върховете на теория графика, могат да имат най-малко две инциденти ръбове. които обикновено не се допуска за геометрични върхове. Има и връзка между геометрични върховете и върховете на кривата. неговите кривина Extrema точки - на върховете на многоъгълника в известен смисъл точки са безкрайно кривина и ако многоъгълника приблизително чрез плавна крива, точките на екстремни кривина ще лежат в близост до върховете на многоъгълника [4]. Въпреки това, приближение многоъгълник с помощта на гладка крива дава допълнителни върхове в точките на минимална кривина.
Плоски плотове мозайки
Vertex планарна мозайка (керемида) - това е точката, в която има три или повече пръстена с мозайка [5]. но не само: най-облицовъчни плочки са също полигони и мозаечни плотове са по върховете на тези плочки. По-общо казано, облицовка може да се разглежда като един вид топологични CW-сложна. Върховете на други видове системи, като например симплициален. - тя е на ръба на нула измерение.
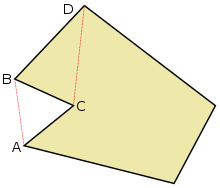
Vertex В е "ухо" като отворен интервал между върховете С и D лежи напълно в многоъгълника. Vertex С е "устата" като отворен интервал между А и В е разположена изцяло извън многоъгълника.
Vertex х I> прост многоъгълник P е основният връх ако диагоналната [X I - 1. х и + 1], X _]> P пресича граници само в точките X I - 1>, и х и + 1>. Има два основни типа на върховете: "ушите" и "отверстията" (виж по-долу). [6].
Главният пик на х I> прост многоъгълник P се нарича "устата", ако диагоналната [X I - 1. х и + 1], х _]> намира извън P.
Броят на върховете на многостен
където V - броят на върховете, Е - броя на ръбовете, и F - броят на лицата. Това уравнение е известно като уравнение на Ойлер. Например, куб 12 има шест лица и ръбове, и следователно - 8 върховете: 8-12 + 2 = 6.
Върхове в компютърната графика
В компютърната графика обекти често са представени като триъгълновиден polyhedra. в която върховете на обекта се сравняват не само трите пространствени координати. но също така и други, необходими за правилното изобразяване на обекта графичен информация като цвят, отразяваща способност. текстура. връх нормали [7]. Тези свойства се използват за изграждане на изображение с помощта на връх шейдъри. Някои от най манипулатор [ен].