Втори ред диференциални уравнения с постоянни коефициенти

Начало | За нас | обратна връзка

На второ място, за диференциално уравнение с постоянни коефициенти на формата:

ако има нула в дясната страна на уравнението,

след това уравнение се нарича хомогенна линейна.

За да реши това уравнение е направена характеристика уравнението. Характеристиката се нарича квадратно уравнение получен чрез диференциално уравнение, където заменя нова променлива К, степента на което се определя по реда на производното:

;

След това - характерен уравнение.

Ние намираме корените на характерното уравнение:

1. Ако характерни корените на уравнението са реални и равни. т.е. deskremenant D = 0, разтворът на диференциално уравнение ще бъде функция от:

2. Ако корените на уравнението характеристика са реални и равни числа. D> 0. след това:

3. Ако корените на характеристика уравнението - комплексни числа с D<0, т.е. . то

Например: Намерете общото решение на диференциално уравнение:

Ние правим до характерното уравнение:

;

Ние намираме корените си:

;

Замени стойността, получена к = 1, уравнение (1), ние получаваме:

.

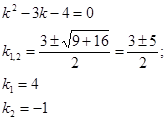
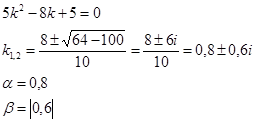
Получените стойности # 945; и # 946; заместител в уравнение (3), получаваме:

5. втори ред диференциални уравнения, които допускат понижаване РЕД

Да предположим, че има диференциално уравнение се решава по отношение на втората производна:

,

Помислете за вида на втория ред диференциални уравнения, които позволяват намаляване на поръчката:

I. Диференциални уравнения не съдържат аргумента:

(*)

замени тази в (*), получаваме:

.

Получихме първия ред диференциално уравнение и решаването му ще включва: или

Споделени променливи, се умножи двете страни по:

.

Въвеждане на заместване: (1)

От уравнение (1) получаваме: (2)

Заместването на стойностите от уравнения (1) и (3) до предварително определена уравнение, и получаване на:

.

Получени първо уравнение ред. Решаването на метода за разделяне на променливите R и у. Уравнението се решава по отношение на P.

.

Намаляване на двете страни от P

.

Разделете променливите, умножаване двете страни, за да получите:

.

Интегриране на двете части:

Замести стойност, получена от уравнението P (4) в уравнение (1), ние получаваме:

Достигнаха първия ред диференциално уравнение в променливите у и х.

Разделете променливите, умножаване двете страни с. получаваме:

.

Ние получи общото решение на диференциално уравнение:

II. Диференциални уравнения не съдържат изискваната функция:

(**)

След това уравнение (**) ще бъде:

.

Разтворът на това уравнение е функция от:

Въвеждане на заместване: (1)

Заместването на стойностите от уравнения (1) и (2) в първоначалното уравнение и получаване на:

.

Разделете променливите, умножаване двете страни, за да получите:

.

Интегриране на две страна на уравнението:

Ние замести стойност F от уравнението (3) в уравнение (1) и получаване на:

.

Разделете променливите, умножаване двете страни с. и да се интегрират:

III. диференциални уравнения, които не съдържат неизвестни функцията и нейната производна:

(***)

Смяна: заместител на (***)

Например: Намерете общото решение на диференциално уравнение:

Въвеждане на заместване: (1)

Заместването на стойностите на уравнение (2) в първоначалното уравнение:

.

Разделете променливите, умножаване двете страни чрез получаваме:

.

Решаване на уравнението, получена чрез интегриране на две части:

Замести стойност F от уравнението (3) в уравнение (1), ние получаваме:

.

Разделете променливите, умножаване двете страни с. и да се интегрират:

.

Забележка. Решаване на интеграл чрез интегриране по части: